Origammli
- 07.16.08
- Sonstiges
- 3 Comments
Neulich im Büro kommt Jörg zu mir und hält stolz wie ein Schneekönig ein Stück Papier in die Luft.
Anstatt wie gewohnt gleich auf die Knie zu fallen und seinen Namen zu preisen, durchbohrt ihn mein fragender Blick. Er erklärt mir, dass sein Programm gerade kompiliert wird und er daher Zeit hat sich mit dem Finden von Antworten auf die Fragen dieser Welt zu beschäftigen – lobenswert.
Im nächsten Augenblick erzählt mir Jörg, er habe es mit genau zwei Faltungen geschafft aus einem handelsüblichen Post-it (der nicht neudeutsche Term ist wahlweise Haftnotiz oder Klebezettel) einen Drachen zu bauen.

Hier mal eine Mini Dokumentation zum Faltprozess. Ich hab zum Größenvergleich eine ca. 20 cm große Mutter daneben gelegt, wie sie auf Ölförderplattformen eingesetzt wird.
Ich merke wie meine Gedanken versuchen weg zu driften und ich stelle mir Jörg vor, wie er von seinem Drachen durch eine plötzliche Windböe weggerissen wird.
Der Wiedereintritt in die Realität ist abrupt, als Jörg mir flacher Hand auf das frisch geknickte Papier schlägt um anschließend den Knick durch eine Wischbewegung der Handfläche entlang der Tischoberfläche durch das Papier zu treiben. Tatsächlich hat er sein kleines Wunder gerade mit einem meiner Haftnotizen wiederholt. Ich bemerke das, weil meine Klebezettel neongelb während seine orange sind („seine“ orangenen lagen vor meinem Urlaub auch auf meinem Schreibtisch, aber die Leipziger hatten so lange nichts, da kann ich als versorgungsverwöhnter Westdeutscher ruhig mal etwas kürzer treten).
Robert kommt herein und findet uns unproduktiv und über einem Haufen von Deltoiden, wie das Drachenviereck streng mathematisch heißt. „Nur zwei Faltungen“ erläutert Jörg herausfordernd, während er das wahrscheinlich kleinste Origami der Welt in seinen Fingern dreht.
Bis in die Haarspitzen motiviert es ihm gleich zu tun, reist Robert das oberste Blatt seines post-it Blocks herunter und beginnt es wieder und wieder zu falten. Obwohl es – Jörgs Symmetrieliebe vorausgesetzt – vielleicht nicht einmal 30 sinnvolle Möglichkeiten gibt ein Blatt Papier zwei Mal zu falten (hiermit sind Äquivalenzklassen von Lösungen gemeint, die durch Bewegungen oder Symmetrien auseinander hervorgehen), gibt Robert bereits nach wenigen Minuten genervt auf.
Nachdem Jörg sein Exemplar noch zweimal auseinander und wieder zusammen gefaltet hat, wofür er inzwischen nicht einmal mehr 28 Sekunden benötigt, ist auch Robert dem Drachenwahn erlegen und versucht aus einem DinA4 Blatt ein Drachen in noch nicht dagewesener Größe zu fertigen.
Erschrocken stellen wir fest, dass sich nicht annähernd das erwartete Resultat einstellt. Dieses Viereck besitzt keine zwei Paare gleich langer benachbarter Seiten. Das Problem musste am Seitenverhältnis liegen. Tatsächlich ergibt sich aus einfachen geometrischen Überlegungen, dem Satz des Pythagoras und dem Termumformungsvermögen eines Neuntklässlers folgende Argumentation:
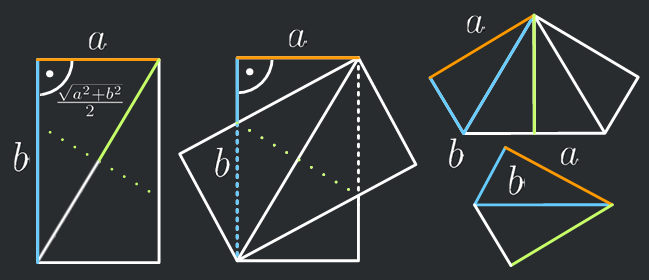
Das hätte jedes Schulkind berechnen können... Der erste Knick erfolgt durch die grün gepunktete Linie, der zweite durch die durchgängige grüne.
Somit muss für das Verhältnis von Langer Seite 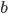 zu kurzer Seite
zu kurzer Seite 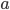 verlangt werden
verlangt werden 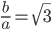 , um einen perfekten Deltoid falten zu können. Bekanntlich ist das Seitenverhältnis beim DinA4 Format
, um einen perfekten Deltoid falten zu können. Bekanntlich ist das Seitenverhältnis beim DinA4 Format 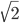 , weshalb der Versuch bei Verwendung dieses Formats zum Fehlschlag führt.
, weshalb der Versuch bei Verwendung dieses Formats zum Fehlschlag führt.
Ein sehr schönes und schön geschriebenes Stück unwissenswertes Wissen. Besonders hübsch find ich die Tatsache, dass jemand in der Lage ist, ein Programm zum Kompilieren zu bringen, Drachenbau neu zu erfinden, einen elitären Kreis Jünger aufzubauen...und Robert dann schon zur Arbeit kommt.
Den lobenswerten Überlegungen zum Trotz ist dieses entstehende Drachenviereck leider fürs menschliche Auge unästhetisch, nur der Mathematiker erkennt dessen Schönheit (Winkel 60 90 90 120, Teilung der langen Diagonal 3:1, Verhältnis der Diagonalen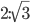 ).
).
Betrachten wir aber nun ein anderes rechteckiges Stück Papier, z.B. A4. Obwohl dieses Seitenverhältnis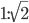 nun wirklich rar gesät ist, lernt man im Kindergarten (zumindest im Ostdeutschen), mit 2 Faltungen einen Drachen zu falten, der zudem durch übermäßige Größe auffällt. Ästhetisch angenehmer fürs Auge überzeugt dieser auch noch mathematisch (Winkel: 45 90 90 135). Wie die Faltung dazu aussieht, dürft ihr ja nommel überlegen.
nun wirklich rar gesät ist, lernt man im Kindergarten (zumindest im Ostdeutschen), mit 2 Faltungen einen Drachen zu falten, der zudem durch übermäßige Größe auffällt. Ästhetisch angenehmer fürs Auge überzeugt dieser auch noch mathematisch (Winkel: 45 90 90 135). Wie die Faltung dazu aussieht, dürft ihr ja nommel überlegen.
Desweiteren gilt für alle Rechtecke mit einem Seitenverhältnis größer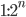 (für
(für 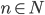 ), dass n Faltungen ausreichen, um ein Drachenviereck zu erhalten. Diese Anwendung mag trivial erscheinen, doch zeichnet sich die erhaltenen Drachen genauso durch drachentypisches Verhalten aus, wie der
), dass n Faltungen ausreichen, um ein Drachenviereck zu erhalten. Diese Anwendung mag trivial erscheinen, doch zeichnet sich die erhaltenen Drachen genauso durch drachentypisches Verhalten aus, wie der 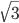 -Drachen.
-Drachen.
Einen schönen Herbst.
Jaja, spotte du nur über meine Arbeitszeiten...
Heute isser übrigens nicht da, d.h. wir verschieben das ausprobieren auf nach meinem Urlaub, oder so...
[...] Martin hat auch eine schöne Abhandlung über Drachenkonstruktionen aus Papier geschrieben. Eine andere, ähnliche Episode aus unserem Arbeitsleben. Posted in Arbeit, computer, deutsch, [...]